Everything on this planet will eventually lose its original excitement and fail your expectations, except Simon Tatham's Puzzles, a series of 40 little games you can play. They're simple but maintain their pleasure over time, particularly "Net", a water-trickling tile-rotating game.

Introducing Net

You're given a big square of N side length, and each little square inside has a type of water pipe. Your job is to rotate each of these small squares until all the pipes line up so that no water leaks from any pipe, and every single square is filled with water. The center square emits all the water.

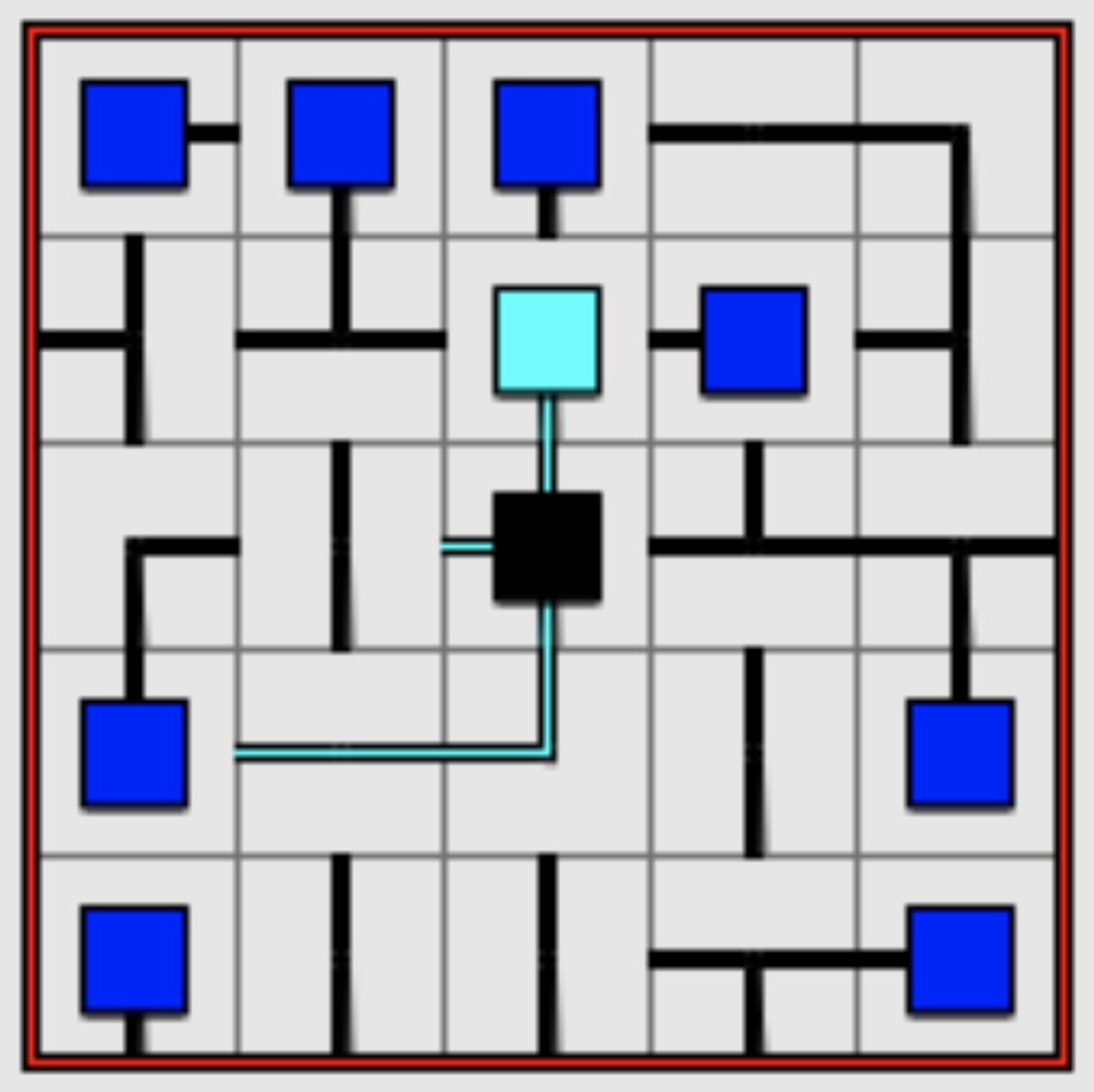
Figure 1: An example game. The center square, which outputs water, is black. Water is cyan (light blue).

As you can see, there are different types of pipes. There are T-shapes with 3 segments; bends with 2; lines with 2; and water sources with 1, denoted by blue squares.

By rotating squares, you eventually get to Figure 2, which is the answer.

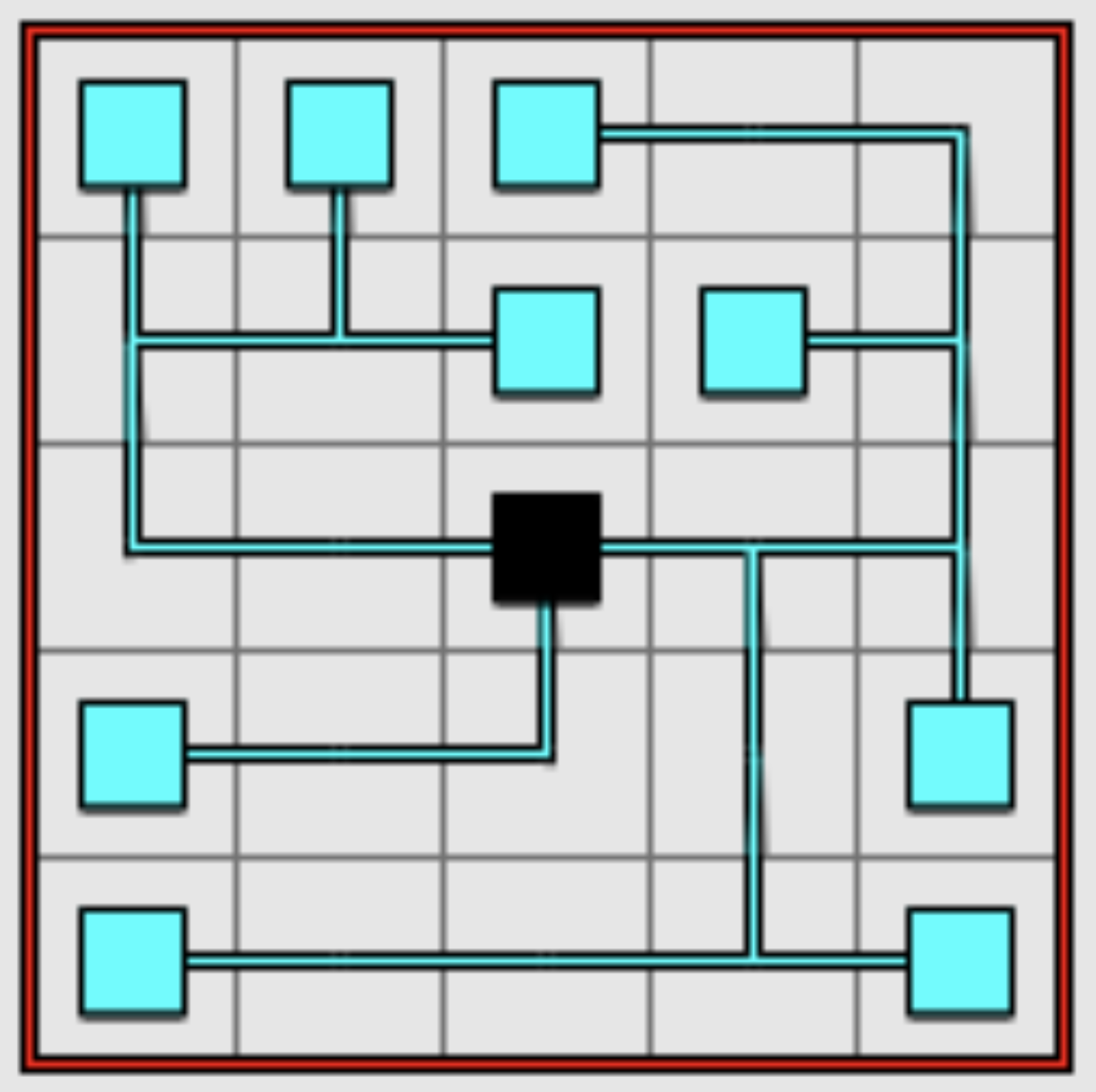
Figure 2: The unique correct answer to the puzzle.

First, I present two optimization formulations for solving Net. I coded these in Julia, so we use the vastly superior 1-indexing!² Also, when describing dimensions, rows comes before columns. Afterwards, I describe the tips I use for solving Net without hesitation or guesswork. If you want to skip to it right away, it's the section "Solving for Enjoyment".

Intuitive Optimization

Notice that each square has four line segments. Our decision variables will be based on this: 1 if that line segment is present in the unique final solution, 0 if not.

But we cannot make a single array of decision variables, because it would be jagged—vertical segments and horizontal segments are quite different! Instead, we make two arrays of decision variables: one to describe all horizontal pipe segments, one for vertical ones. Call these H(r, c) and V(r, c). Each one is either 1 or 0 depending on whether there will be a pipe segment there in the final solution. We enumerate decision variables as seen in Figure 3. H is a N by 2N matrix; V is a 2N by N matrix.

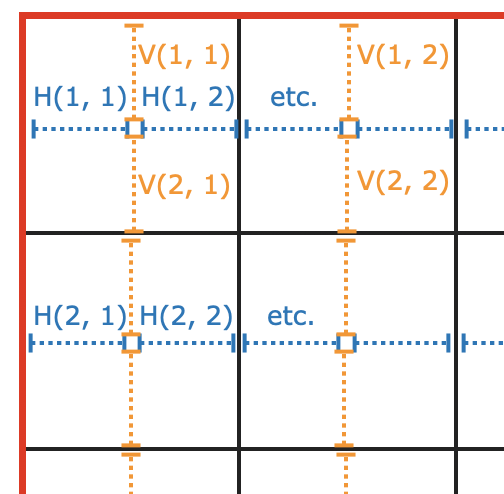
Figure 3: Decision variables for each square's potential segment: blue represents H(r, c) and orange, V(r, c).

Our constraints are as follows: To avoid water leakage, we need inter-square horizontally and vertically adjacent pipe segments to either both be present or absent. For instance, either both V(2, 1) and V(3, 1) are 1, in which case pipe segments go through both dotted orange segments, or both are 0, in which case no pipe segments go through either. If not, water will leak.

Furthermore, the four sides close to the edges of the large square (red lines) must be devoid of pipe segments, because there is nothing they can connect to, and will leak. This means H(1, any column), H(N, any column), V(any row, 1), and V(any row, N) must equal zero.

The decision variables within each square are also constrained by the type of piece present. If it's a T-shape (T), three out of four segments must be 1, while the last must be 0, because there are exactly 3 pipe segments on a T. As a result, our constraint is: sum of decision variables in that square is 3.

Similarly, for water sources (S), the sum of decision variables in that square is 1. The line (L) and bend (B) are a bit more complicated. For L, the pipe segments are opposites, but it's hard to ask a solver to deal with "Either the sum of these two decision variables is 2, or it's 0." Instead, we notice that for each of the 4 adjacent pairs of decision variables (e.g. H(1, 1) is adjacent to V(1, 1)), the sum of decision variables for that pair is 1. Convince yourself that this is an equivalent formulation for L.

Finally, for B, we require the 2 opposite pairs of decision variables to each sum to 1.

Those are all our constraints.

Given a square on the grid, which coefficients represent its decision variables? Well, consider a square on row R and column C.

The horizontal variables are on row R, one on column 2C-1 and one on column 2C. The vertical variables are on column C, one on row 2R-1 and one on row 2R. So for square [R][C], the decision variables are H(R, 2C-1), H(R, 2C), V(2R-1, C), and V(2R, C).

Now it's time to put this all together in code. We first initialize our grid with symbols representing one of the four types, start up a model, and write in all the constraints. The constraints by type of pipe is seen in Figure 4.

Figure 4: Code snippet: Different constraints on decision variables based on different pipe type.

I also created some custom code that will make a beautiful text display of the solution. After running it, we indeed get the solution on Figure 2!

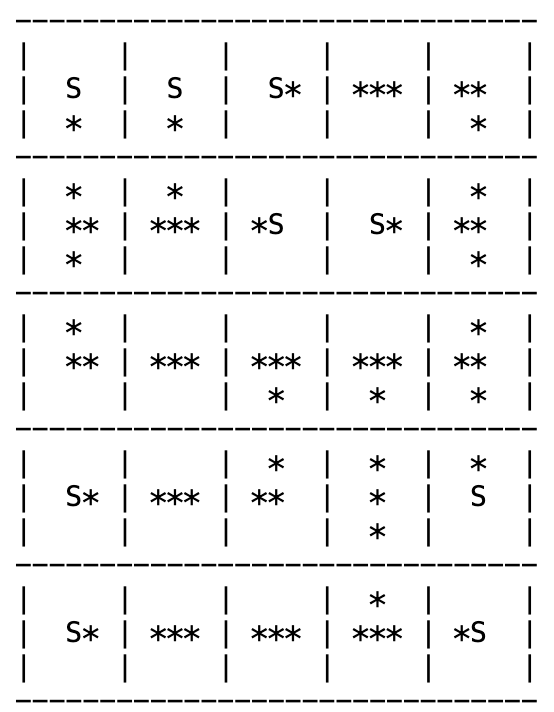
Figure 5: The solution as generated by the HiGHS solver.

Cleverer Optimization

That we must use arrays of such different shape (H and V), and deal with multiplying row and column indices by 2, is clumsy. Noticing that inter-pipe neighbor variables must have the same values anyway, and that pipe segments bordering the big square's sides have value 0, we revisualize to the following, much simpler decision grid!

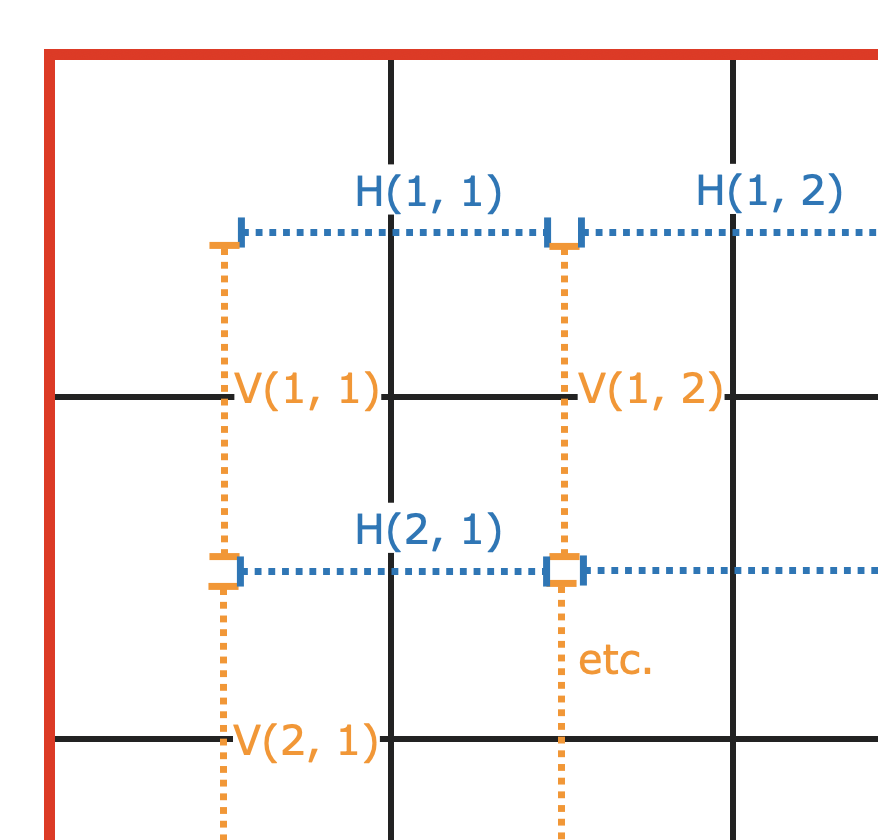
Figure 6: A cleverer decision grid.

Now the constraints are much simpler, as are the variable references. For a square on row R and column C, they are H(R, C-1), H(R, C), V(R-1, C), and V(R, C). Care has to be taken to avoid accidentally 0-indexing with the negative sign, or N-indexing with too much addition.

Now, the only set of constraints we need to establish are those related to the type of pipe. They are exactly the same as before, just with different H and V indices.

This solution is better than the first, because it has 2N²-2N variables as opposed to 4N². The smaller number of constraints will also help runtime. In practice, it is better to intentionally pad the two matrices H and V to be of size (N+1) in one way instead of (N-1), because HiGHS (the JuMP optimizer) cannot handle ternary expressions in constraints, and it's bad to create 8 special cases to deal with the edges of row or column equals 1 or N.

And indeed, we get the same solution.

Solving for Enjoyment

Optimization is great and all, but how about doing it ourselves? I'm a big fan of Net, and I've been playing gradually larger sizes. The most recent one I solved was a 121x121 big boy (that's 14'641 squares), and it took serious time and concentration to wade through it. Figure 7 was the reward.

Figure 7: The labyrinth to end all labyrinths. The 121 by 121 water-trickle problem, solved at last. This is in dark mode. Dark mode is better than light mode!³

The techniques are quite simple, and are as follows:

0. You are allowed to "lock in" squares that you're sure are correct! If you are confident that a certain square must be rotated a certain way, press and hold and its background will turn to a darker gray (instructions may differ by platform). This will help you keep track of which squares you still need to rotate.

1. The edge squares are simple. Just make sure no pipe touches the edge. I recommend that, in the absence of better moves, finish up all the edges and gradually move into the center, because the edges are guaranteed.

2. Since water must flow to all squares, if you have certain pipes "trapped" or "sandwiched" around many source squares, you can know which way they must go. For example, Figure 8 is not allowed, as we form an isolated enclosure without water; as a result, we know that line in the middle must be vertical.

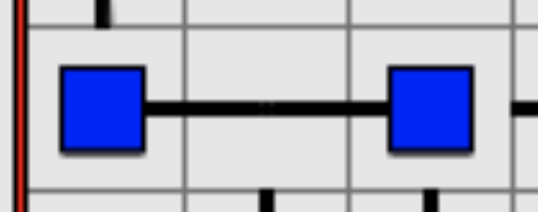
Figure 8: This is prohibited.

3. As a trivial case of technique 2, source nodes cannot face each other!

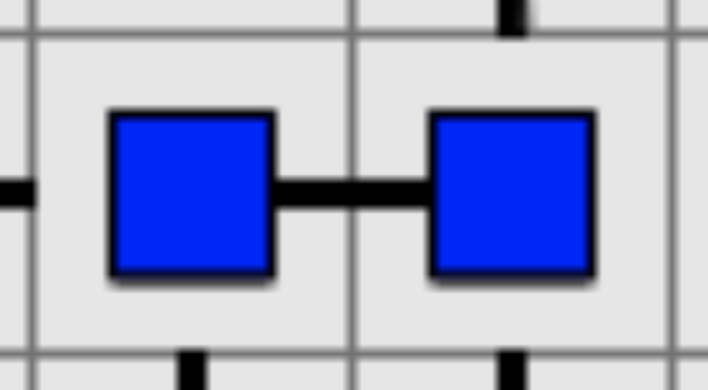
Figure 9: This belongs in a biology textbook, not a computer game.

4. If you've secured a few squares (i.e. are certain they are correct), you might be able to secure others as well. In Figure 10, for instance, securing the T on the right forces the T on the left to be in its displayed orientation; otherwise, a pipe segment will incorrectly touch the left side of the gray square, which is not accepting water.

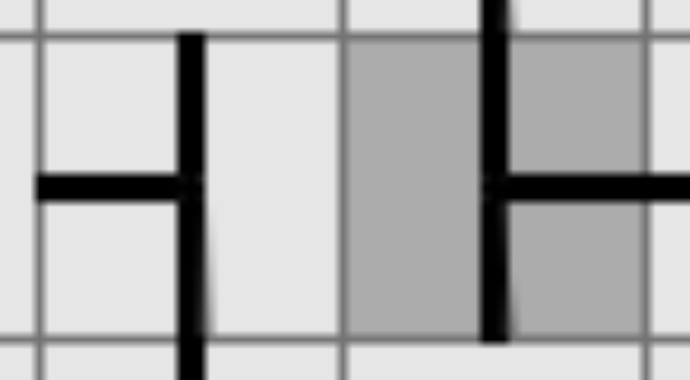
Figure 10: After securing the right T, the left T must be in this orientation.

5. You might not be able to determine for sure which way a pipe should point, but if a pipe has special properties, you might be able to secure some pipes beyond it. See Figure 11 for an example. I don't know whether the bend in the center will be extending right and up or right and down, but no matter what, I know it will not extend left, because one pipe segment of the bend must interact with the T's left segment. Therefore, the line on the left must be vertical. Especially when you have several bends in a line, these cascades can be amusing.

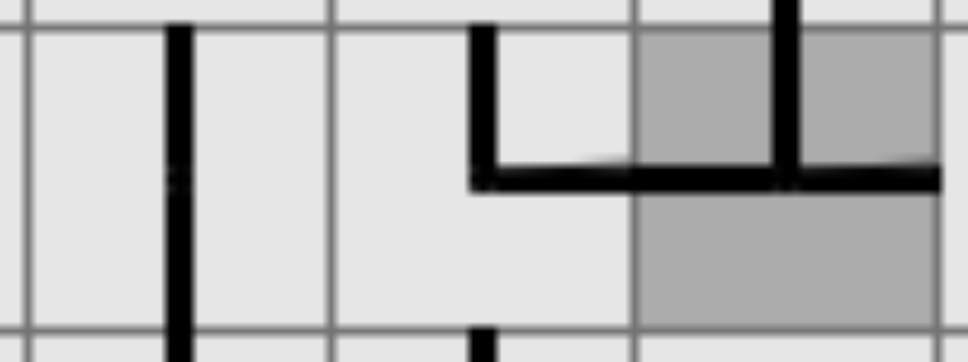
Figure 11: I can't get you directly, so I'm going to quantum tunnel through you.

6. Any type of loop is prohibited and will be marked in red. As a result, if you have a few squares that almost complete a loop, you know they have to face away from each other.

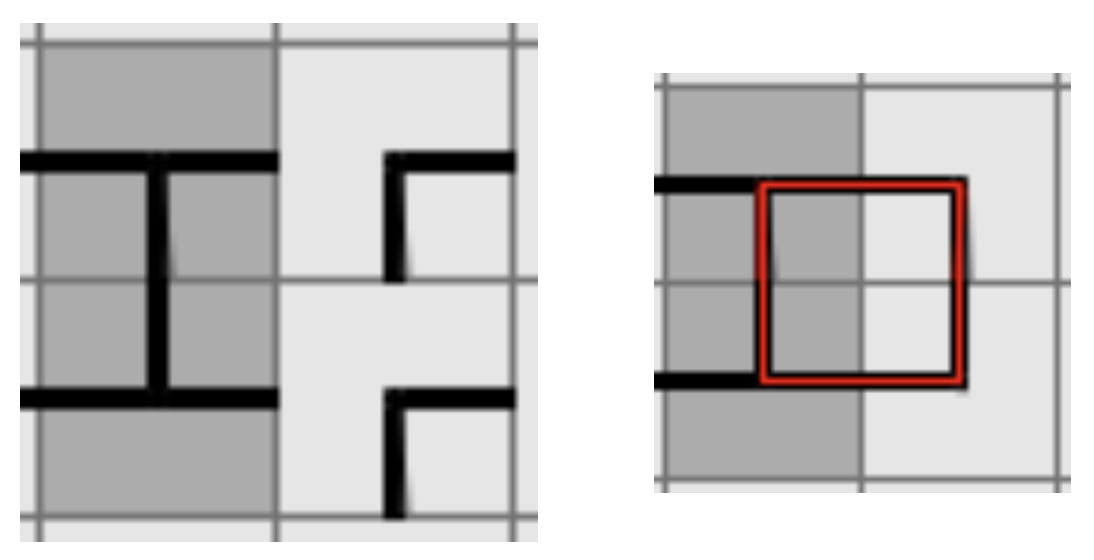
Figure 12: The upper bend must extend left and up; the lower bend, left and down. Both bends must extend left, but if the upper bend extended left and down instead, that would force the lower bend to match the upper bend by extending left and up, creating a loop, which is unacceptable (right).

These rules are what I use to play, and should suffice. Occasionally a few guesses are warranted, and usually, one avenue quickly leads to a loop or a trapped set of pipes.

Conclusion

Net is one of Simon Tatham's nicest puzzles. It's straightforward, simple, and, if extended to sufficiently large grids, satisfying when finally solved. That Net can be configured into an optimization problem also indicates its usefulness. Once you hit 135 by 135 squares or so, the game engine takes awhile to produce a puzzle for you to solve due to the logical and display complexity, but given that those take me several hours (15'000 tiles, 1 tile per second at best, that's over 4 hours!), I'd probably use the clever optimization method. Still, large-scale Net could be fun as a group activity—race to see who fills in the most squares!

The ultimate takeaway: When life gives you trickles of water, hurry up and rotate your squares so you don't let too much water run away!

Footnotes

¹ You can also download them on your favorite device. It's Linux-friendly and can be found on the F-Droid Store too.

² Don't debate me.

³ Don't debate me.