When planning began for the fall 2022 semester at MIT a month ago², my theme was depth. Having scavenged around MIT’s departments and people in the last two years, it was time to go deep. Whether you’d call it “drilling deep” or “descending the depths”, the concept is there. Majoring in 18 (Mathematics) and 6-4 (Artificial Intelligence & Decision-Making), I chose two classes in each.

These were:

18.404 Theory of Computation;

18.675 Theory of Probability;

6.7201 Optimization Methods;

6.8611 Quantitative Methods for Natural Language Processing.

When I went to the lectures and studied the materials, it became apparent I had chosen a synergistic set of classes. One would naturally expect some cohesion between pairs of classes, but not to the extent described in this essay. There’s ‘teaming up’ on classes: taking two classes that, while in different departments, rely on a bedrock of identical material. 8.05 (Quantum Physics II) and 6.830³ (Advances in Computer Vision), for instance, use matrices and linear algebra heavily, despite being separate in purpose and theme. But one can also construct a 'triple team', or in this case, a 'quadruple team'.

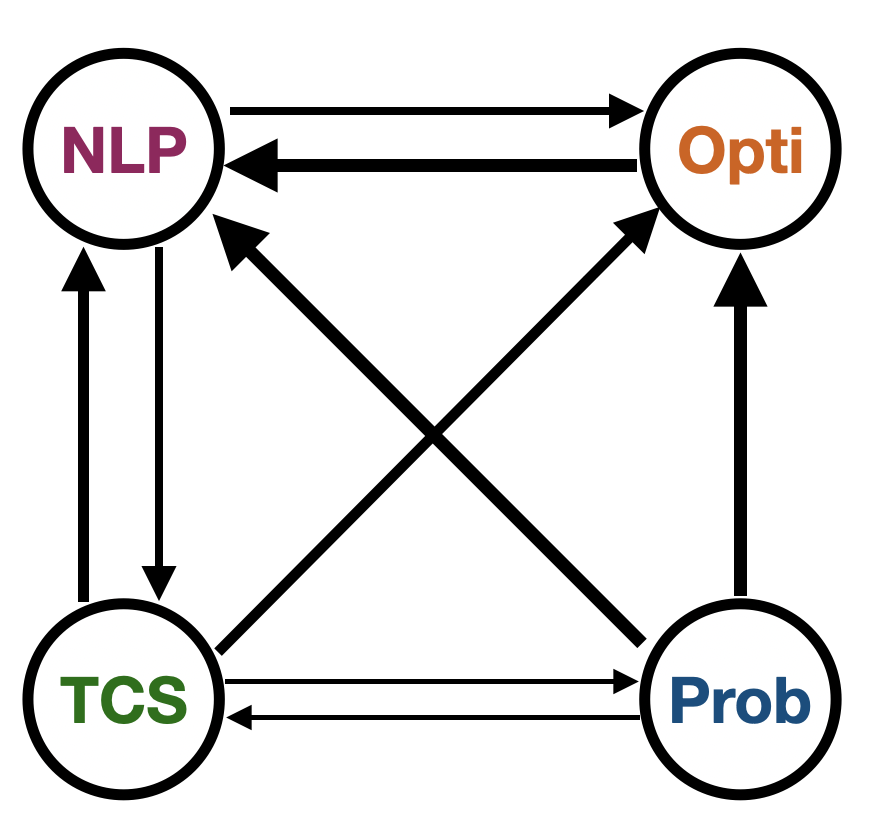
There are the 9 connections between classes⁴, in order of decreasing strength. I will use the abbreviations “TCS”, “Prob”, “Opti”, and “NLP” to avoid writing out long terms.

Opti ↔ NLP: Both of these courses are very intense, with projects, coding-based homeworks, and long presentations with a mix of theory and application. Their similar nature is supported by connections going in both directions.

For Opti → NLP, there are several avenues. Improving runtime of NLP algorithms, especially gradient descent and training data, are common tasks in undergraduate machine learning courses. Computation of heuristics amidst an ‘engineering-like’ field of study is relatively more welcome than in other, more proof-based classes. I refer to ML as engineering-like, as the majority of work is comprised of finding models that work and explaining their results; why they work is left to either the void or theoretical ML researchers. This latter group engages with questions on why ML works as it does, and is relatively understudied compared to the engineer-type ML.

For NLP → Opti, there’s two main avenues. First: when faced with an optimization problem, should we use the primal or the dual? Given some form of constraints, an algorithm could decide which formulation to use by training on problems for which the better formulation is known⁵. Second: in robust optimization, what should we set our gamma parameter to (i.e. how much uncertainty will we allow in modeling)? If we had significant historical data, we could use part or all of it as training and testing set material for different gamma values, and based on validation results, determine our gamma⁶.

Prob → Opti: There exists a branch of Opti, robust optimization, which quantifies how likely stochastic constraints are to be satisfied given a loss tolerance on the objective. Prior to this, there was no variance allowed in parameters; robust optimization turns optimization from a science to more of an art, as the concept of ‘how much risk are we willing to tolerate’ is a fluid, usually societal question. A particularly niche application, two-stage (or adaptive) optimization, is today’s furthest push into robust optimization.

TCS ↔ NLP: One would expect, given terms in TCS like “context-free grammar” and “regular language”, that such endeavors are relatable or extendable to language or linguistics at large. This is not the case. The only resemblance between the two enterprises is in CFGs—when building tree models for sentences in NLP, CFGs are written and involved. Otherwise, the depth in the two classes branches off (mind the pun). In TCS, complexity theory is further studied; this is mentioned in passing several times in NLP. In NLP, more algorithms, models, and refinement of research is explored, which has no analog in TCS. However, the spirit of TCS—proving results and explaining why—could help lead theoretical ML work (see “Opti ↔ NLP”).

Prob → NLP: The keystone of good machine learning is probability, and this applies for NLP. At large, NLP is word generation—whether translation, summarization, fill-in-the-blank—and this depends on choosing the highest-probability possibility.

TCS → Opti: The link is complexity. In optimization, the hardest task is finding algorithms (i.e. solutions) that are scalable, robust, and fast. Analyzing the runtime of an optimization algorithm relies on principles from complexity analysis.

Prob ↔ TCS: There’s not much connection here, bar the high-level observation that both classes revolve around theory. In solving problems for these two classes, one needs first to understand the material presented in the textbook, and then the solution will come ‘naturally’. It is easy to know where a solution is lacking once one internalizes the material; from an outsider’s perspective, this is impossible to determine, and the nagging questions of “How did you know to do this?” and “How should I write it to avoid this issue?” appear.

The relative strength diagram of these 12 connections is given below, with a thicker arrow indicating more connectivity. Overall, it appears NLP has the strongest connections with all classes. The diagram also indicates I chose a good slate of classes, as they were interconnected in almost all possible ways. As it stands, the old adage holds: All 4 One and One 4 All!

Class Connectivity

Footnotes

¹ I am aware that “quadriplex” does not mean “consisting of four parts”. But given how I used “triplex” in my article ”The Triplex Mindset”, I will use “quadriplex” here, if only in the hopes I can get “quadriplex” to mean what it intuitively should!

² Back when I wrote the first version of this article, it would have been August 2022.

³with the new MIT course numbering. In the old numbering, this would’ve been 6.869.

⁴There should be 6 * 2 = 12 connections, but three of the 6 class links are unidirectional.

⁵This is the connection Prof. Alexandre Jacquillat explained to me in a conversation we had.

⁶An example of similar nature was presented by Benjamin Boucher in Optimization class.